동역학 시스템
동역학 시스템은 운동하는 물체에 적용되는 힘, 가속도, 속도, 위치 등 물리적인 변수들의 관계를 의미한다.
$$F=ma $$
$$v(t) = v(0)+\int_0^t a(t)dt$$
$$x(t)=x(0)+\int_0^t v(t)dt$$
지금까지 많이 봐 왔던 뉴턴 제2법칙은 동역학 시스템의 기본이 되는 모델이다. 위 수식에서 출발하여 좀 더 자세하게 동역학 시스템을 모델링 하는 방법을 공부할 것이다.
Mass - Spring - Damper System
모든 자연계에는 저항이 존재한다. 물체가 운동할때도 마찬가지로 움직임을 방해하려는 힘이 있다. 마찰력, 공기저항등이 있다. 마찰력은 물체가 움직일때 변위의 변화에 비례하여 저항하는 힘이고, 공기저항은 속도의 변화에 저항하는 힘이다. 이처럼 모든 운동에는 위치 변화에 저항하는 힘과 속도 변화에 저항하는 힘이 존재한다. 이를 다음과 같이 Mass-Spring-Damper로 모델링할 수 있다.
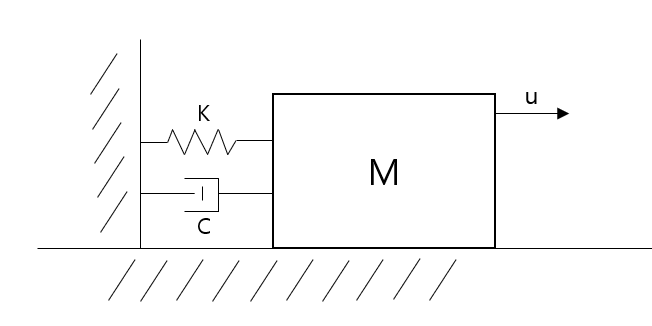
$ M :$ Mass
$ U :$ External Force
$ K :$ Spring coefficient
$ C :$ Damping coefficient
이 물체의 변위를 x라고 하면 운동 방정식은 다음과 같다.

$$ M\ddot{x} = -Kx - C\dot{x} +u$$
$$ M\ddot{x}+C\dot{x}+Kx=u$$
이는 외력이 작용하는 물체의 일반적인 동역학 시스템을 미분 방정식으로 모델링 한 것과 같다. 예상컨데, 이 시스템은 초기값이 있을 경우 진동하다가 점차 정지할 것이다. 이때 과연 얼마나 진동할지, 언제 정지할지, 어디에 정지할 지 알 수 있을까? 그것을 알아가는 과정이 자동 제어의 과정이 된다. U에 대하여 K, C에 따라 달라지는 물체의 운동을 분석하고 적절한 K와 C를 선별하여 제어기를 설계하는 과정이 자동 제어이다.
How to Solve
이 시스템의 운동을 알기 위해서 위 미분 방정식의 해를 구해야 한다. 미분 방정식의 해는 물체의 시간에 대한 변위의 함수
$x\big(t\big)$이다. 외력이 없는 경우 다음과 같다.
$$Assume. \ u=0 \rightarrow x=Ae^{st}$$
$$MAs^{2}e^{st}+CAse^{st}+KAe^{st}=0$$
$$Ae^{st}(Ms^{2}+Cs+K)=0 $$
이때 $e^{st} \neq 0$ 이므로 $Ms^{2}+Cs+K=0 $을 만족하는 s값을 찾으면 된다.
$s=\frac{-C\pm\sqrt{C^{2}-4MK}}{2M}$
이때 $\omega = \sqrt{\frac{K}{M}}, \ \zeta=\frac{1}{2}\frac{C}{\sqrt{MK}}$로 치환하자.
$$ s=-\zeta\omega\pm \omega\sqrt{\zeta^{2}-1}$$
이때 s는 $\zeta >1$인경우 두 개의 실근,
$\zeta =1$인 경우 중근
$\zeta <1$인 경우 켤례 복소 근을 갖는다.
미분방정식의 해는 $x(t) = C_1e^{s_1t}+C_2e^{s_2t}$이다.
그러므로 s가 실근과 중근의 경우, x가 수렴하기 위한 조건은 s의 크기가 음수이면 된다.
그러나 s가 켤례 복소근일 경우 x의 수렴 조건을 계산하기가 복잡해진다.
이 경우, s는 $ s=-\zeta\omega\pm j\omega\sqrt{1-\zeta^{2}}$라고 할 수 있다.
미분방정식의 해는 $ x=A_1e^{-\zeta\omega+ j\omega\sqrt{1-\zeta^{2}}}+A_2e^{-\zeta\omega-j \omega\sqrt{1-\zeta^{2}}}$이다.
2차 미분 방정식 해는 두개의 독립적인 기저[더하고 뺌]로 다시 구성할 수 있으므로 다음과 같이 쓸 수 있다.
$x(t) = A_1\big((e^{-\zeta\omega+ j\omega\sqrt{1-\zeta^{2}}}+e^{-\zeta\omega-j \omega\sqrt{1-\zeta^{2}}})\big)+A_2j\big((e^{-\zeta\omega+ j\omega\sqrt{1-\zeta^{2}}}-e^{-\zeta\omega-j \omega\sqrt{1-\zeta^{2}}})\big)$
이때 Euler Formula $e^i\theta = cos(\theta)+isin(\theta)$ 를 이용하면 다음과 같이 정리된다.
$x\big(t\big)=2A_1e^{-\zeta \omega}cos(\omega\sqrt{1-\zeta^{2}t}) - 2A_2e^{-\zeta \omega}sin(\omega\sqrt{1-\zeta^{2}t})$
$=2e^{-\zeta \omega}\big(A_1cos(\omega\sqrt{1-\zeta^{2}t})-A_2sin(\omega\sqrt{1-\zeta^{2}t})\big)$
삼각 함수 합성 공식을 이용하여 다음과 같다.
$x=Ae^{-\zeta\omega t}sin(\omega\sqrt{1-\zeta^2}-\phi)$
$\zeta :$ damping ratio
$\omega :$ natural frequnecy
$\phi :$ phase
이는 exponential 함수와 sin 함수의 곱으로 이루어 져 있으므로, sin으로 진동하면서 exponential에 의해 진폭이 변한다고 볼 수 있다. 그러므로 x의 수렴 조건은 s의 실수부가 음수이어야 한다. 그렇지 않을 경우 물체는 진동하다가 점점 진폭이 커지고 결국 발산하게 된다.
정리하면, 특성방정식의 근의 실수부가 음수(복소 평면에서 왼반면)에 존재해야 물체가 특정 위치에 수렴한다는 것을 알 수 있다. 이 사실은 자동제어 전반에 걸쳐 중요한 개념이다.
Analysis
위 미분 방정식의 의미를 좀 더 살펴보자.
$$ M\ddot{x}+C\dot{x}+Kx=u$$
$$\omega = \sqrt{\frac{K}{M}}, \ \zeta=\frac{1}{2}\frac{C}{\sqrt{MK}}$$
$$\rightarrow \ddot{x}+2\zeta\omega\dot{x}+\omega^2x=\frac{u}{M}$$
$$solution : x=Ae^{-\zeta\omega t}sin(\omega\sqrt{1-\zeta^2}-\phi)$$
s가 실근일 경우 수렴하는 조건은 매우 간단하기 때문에 큰 관심이 없다. s가 켤례 복소 근일 경우에 x는 $ \omega$ 와 $\zeta$에 따라 어떻게 변할까? 그래프로 그려서 살펴보자.
% matlab
t = linspace(0,10,10000);
m=1;
k=1;
c=0;
w = (k/m)^0.5;
zeta = c/(2*w);
x = exp(-zeta*w.*t).*sin(w*(1-zeta^2)^0.5.*t);
plot(t,x,'r')
yline(0)
legend('m=1, k=1, c=0')
xlabel('time (sec)')
ylabel('Amp')
grid on
grid minorCase ①. M=1, K=1, C=0
damping coefficient는 0이고 sping coefficient만 존재한다고 하자.
natural frequency $\omega=1 rad/s$, damping ratio $\zeta=0$ 이다

damping ratio가 0이므로 진폭이 감쇠하지 않는 것을 볼 수 있다.
Case ②. M=1, K=3, C=0
K가 증가하면 어떻게 될까? 이때의 $\omega = \sqrt{3}, \zeta=0$

진동수가 증가한 것을 알 수 있다. 그럼에도 불구하고 물체는 감쇠하지 않고 진폭이 일정하게 진동한다. 이 상태에서 제어 변수 x를 0으로 수렴시키고 싶다면 어떻게 해야할까?
Case ③. M=1, K=1, C=1
이때의 $\omega=1 rad/s$, damping ratio $\zeta=0.5$이다

x의 진폭이 줄어들면서 0에 수렴한다! x의 solution에서도 알 수 있듯이 x는 $e^{-\zeta\omega t}$에 의해 진폭이 감소하고 $sin(\omega\sqrt{1-\zeta^2}-\phi)$에 의해 진동수가 $\omega\sqrt{1-\zeta^2}$로 감소한다. c가 더 커지면 어떻게 될까
Case ④. M=1, K=1, C=1.5

제어변수 x의 진폭이 더 감소했고 더 안정적으로 0에 수렴하는 것으로 보인다!
그래프를 한번에 비교하면 아래처럼 그려진다.

여기서 알 수 있는 것은, 모델의 진동이 감쇠하는 속도와 진동수를 M,K,C,로부터 조절할 수 있다는 것이다. 즉 설계자가 원하는 제어 목표를 원하는 값에 원하는 형태로 수렴하기 위해서 적절한 계수 M,K,C를 찾으면 되는 것이다. 이 글에서 설정한 제어 목표는 물체의 위치 x이었지만, 같은 방식으로 로켓의 속도나 자동차의 위치 등을 제어할 수 있다면 자율 주행이 가능해 진다.
이번 글에서는 모델의 미분방정식을 대입법으로 풀었기 때문에 수식이 복잡하고 어려워 보일 수 있다. 하지만 다음 글에서 Laplace Transform을 공부하게 되면 해를 구하는 쉬운 방법을 사용할 수 있다. 또한 나중에는 m,k,c를 하나씩 대입해 보는 것이 아니라 다른 방법으로 m,k,c를 바로 구하는 방법을 배울 것이다.
자동제어라는 과목은 결국 적절한 M,K,C를 구하는 방법이다. 이 글에서는 입력을 0으로 가정하였지만 실제로는 외력이 존재한다. 당연히 물체를 움직이기 위해서는 외력이 존재하고 그에따라 물체가 움직이게 된다. 앞으로는, 외력을 가했을 때 물체가 어떻게 움직일지 분석하는 방법과 그 움직임을 안정적으로 만들기 위해 M,K,C를 설정하는 방법을 공부할 것이다.
