Intro
앞 글에서 vector, matrix, function의 norm에 대해 공부했다. 이번 글에서는 선형 시스템의 norm을 공부한다.
System norm은 control law를 설계하기 위한 중요한 조건으로 변환될 수 있으며, System norm을 어떻게 설계하는지에 따라 시스템의 안정성과 최적성을 결정할 수 있다. 그렇기 때문에 system norm에 대해 잘 이해하고 있어야 한다.
Induced $L_2$ norm of the system
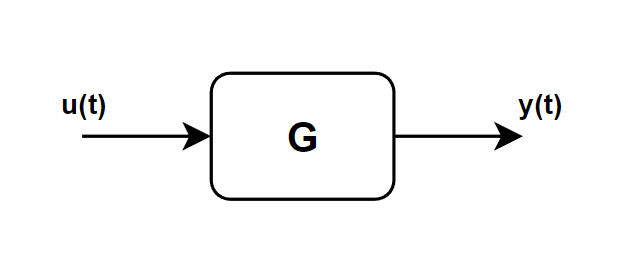
$$L_2=||g(t)||_2 \triangleq \underset{u\in L_2}{max}\frac{||y(t)||_2}{||u(t)||_2}$$
- Definition of $L_2$ stable
A system $G(s)$ is $L_2$ stable or externally stable if for every $u(t) \in L_2$, the output $y(t)$ is in $L_2$
For a linear system
$$Y(w)=G(w)U(w)$$
$$\downarrow$$
$$||Y(w)||_2=||G(w)U(w)||_2 \leq \bar\sigma(G(w))||U(w)||_2$$
$$Because \;\; \bar\sigma(G(w)) \leq \underset{w}{max}\bar\sigma(G(w)),$$
$$||Y(w)||_2 \leq [\underset{w}{max}\bar\sigma(G(w))]||U(w)||_2$$
Apply Parseval's theorem,
$$||y(t)||_2 \leq [\underset{w}{max}\bar\sigma(G(w))] ||u(t)||_2$$
$$\therefore \frac{||y(t)||_2}{||u(t)||_2} \leq \underset{w}{max}\bar\sigma(G(w))$$
$$\text{This hold for any } u\neq0,\in L_2$$
The equality is holds when
$$ \underset{u}{max}\frac{||y(t)||_2}{||u(t)||_2} = \underset{w}{max}\bar\sigma(G(w)) $$
H norm of transfer function
- $H_{\infty}$ of $G(w)$
Single-Input-Single-Output (SISO) : $||G||_\infty \triangleq \underset{w}{max}|G(w)|$
Multy-Input-Multy-Output (MIMO) : $||G||_\infty \triangleq \underset{w}{max}\bar\sigma(G(w))$
- $H_2$ of $G(w)$
$$ \text{SISO : } \;\;||G(s)||_2 \triangleq \sqrt{\frac{1}{2\pi}\int_{\infty}^{\infty}|F(w)|^2dw}$$
$$\text{This can be founded from square of Bode plot}$$
$$\text{MIMO : } \;\; ||G(s)||_2 \triangleq \sqrt{\frac{1}{2\pi}\int_{\infty}^{\infty} tr(G^*(wj)G(wj))dw}$$
Let $g(t)$ is the impulse response of $G(s)$, then $g(t)=\mathcal{L}^{-1}(G(s))$.
By Parseval's theorem,
$$||g(t)||_2=||G(s)||_2$$
$H_2$ norm can be obtained from impulse response.
- $H_2$ norm using controllability and observability gramian
$$g(t)=\mathcal{L}(G(s))=Ce^{At}B$$
$$||G(s)||_2=||g(t)||_2=\int_0^{\infty}tr(g^*(\tau)g(\tau))d\tau=tr[B^T\int_0^{\infty}e^{A^T\tau}C^TCe^{A\tau}d\tau B]$$
$$=tr(B^TQB), \quad Q \textit{ : Observability gramian}$$
$$=\int_0^{\infty}tr(g(\tau)g^*(\tau))d\tau=tr[C\int_0^{\infty}e^{A\tau}BB^Te^{A^T\tau}d\tau C^T]$$
$$=tr(CPC^T), \quad P \textit{ : Controllability gramian}$$
P, Q are the solution of
$$\begin{cases} A^TQ+AQ+C^TC=0 \\ AP+PA^T+BB^T=0 \end{cases}$$
- $H_2$ norm space
$H_2$ space is the set of transfer function $G(s)$ of analytic in RHP and bounded with $H_2$ norm
For $G(s)=\frac{a(s)}{b(s)}$, $H_2$ space is the set of stable and strictly proper transfer function
* Anylytic in RHP : If derivative of $G(s)$ exists in RHP ( no pole in RHP ).
- $H_\infty$ norm space
$H_\infty$ norm space is set of transfer function of analytic RHP and bounded with $H_\infty$ norm.
And the set of stable and proper transfer function.
