Intro
Attitude Kinematics란 위성의 회전, 이동에 따라 변화하는 위성의 자세 변화에 대한 관계들이다. 위성이 회전하고 있다면 분명히 자세는 변화하고 있는 것이다. 얼마나 어떻게 변하고 있는 것일까? 그리고 이 것을 어떻게 표현할 수 있을까.
앞 글에서 위성의 자세를 표현하기 위한 방법으로 euler angle, quaternion, DCM을 공부했다. 그렇다면 자세의 변화란 이 값들이 변한다는 것이고, 자세의 변화는 이들의 시간 미분으로 표현할 수 있을 것이다. 자세 변화를 계산해 내었다면 위성의 dynamics와 함께 자세 제어에 이용할 수 있게 된다,
Attitude Kinematics
- 이동 (Translation)
위성의 이동은 위치, 속도와 관련이 있다. 위치의 미분은 속도라는 것은 알고있을 것이다.
위치 : $\vec{r}$
속도 : $\vec{v}$
$$\frac{d\vec{r}}{dt}=\vec{v}$$
그러나 이 관계는 관성 좌표계에서만 유효하며 비 관성 좌표계에서는 유효하지 않다.
어떤 물체의 위치를 표현하기 위해서는 기준이 필요하다고 언급한 적 있다. 이때 기준은 회전하거나 가속해서는 안된다. 만약 어떤 벡터가 표현된 좌표계가 회전하거나 가속한다면, 그 좌표계의 회전 또한 벡터의 변화에 반영해 주어야 한다. b-frame에서 표현된 벡터 $\vec{r}_b$가 를 정의하자. 기준 좌표계인 r-frame으로부터 b-frame의 각속도를 $\vec{w}_b$라고 한다면 벡터 관계는 다음과 같다.
$$\frac{d\vec{r}_r}{dt}|_r=\frac{d\vec{r_r}}{dt}|_b +\vec{w_b} \times \vec{r}_r$$
위 식에 대해 완벽히 이해하고 있어야만 앞으로 동역학을 쉽게 다룰 수 있다. 반드시 이해하고 넘어가기를 바란다.
- 회전 (Rotation)
위성의 회전은 각도, 각속도와 관련이 있다. 각도의 미분은 각속도가 될 것이다. 과연 그럴까?
각도를 어떻게 정의하는지에 따라 맞을 수 도, 아닐 수 도 있다. 우리가 지금까지 정의한 각도는 eular angle 뿐이다. 앞의 글에서 다루었듯이 Eular angle의 미분은 각속도가 아니다. Eular angle은 eci frame에서 body frame으로의 회전 각도 이고 각속도는 body frame에서 위성의 anguler rate이기 때문이다. 이 둘은 전혀 다른 개념이다.
그렇다면 위성의 회전은 어떻게 표현할 수 있을까. 가장 직관적인 방법은, eular angle의 미분을 유도하는 것이다. 이는 위성의 각속도와는 다른 개념이다. 이와 관련된 내용은 이미 앞 글에서 다루었으므로 이 글을 참고하기를 바란다.
2023.03.07 - [비행동역학 및 제어] - [비행동역학 및 제어] 1. 기준 좌표계 및 좌표계 변환
[비행동역학 및 제어] 1. 기준 좌표계 및 좌표계 변환
비행체의 상태를 표현하기 위해서 기준 좌표계가 필요하다. 기준 좌표계는 설정하는 사람마다 다를 수 있으나, 표현된 물체의 절대 위치는 동일해야 한다. 항공우주 공학에서 사용되는 대표적
dongmin-archive.tistory.com
다른 방법으로는 DCM, quaternion의 변화를 유도하는 것이다. 위성의 자세 제어 측면에서 오일러각 보다 DCM이나 쿼터니안을 사용하는 것이 훨씬 효율적이기 때문에 이들의 Kinematics를 자세 제어에 활용하게 된다.
Euler's Rotation Theorem (Direct DCM method)
b-frame의 각속도와 회전 각을 통해 직접적으로 DCM을 유도하는 방법이다. 이름이 Euler's Rotation Theorem 이기에 오일러 각을 사용하는 것으로 착각할 수 있지만, 그렇지 않다. 오일러각을 사용하지 않으며 단지 회전축 벡터와 회전각 두 가지 만을 사용하여 DCM을 만들어내는 방법이다. 쿼터니안 개념과 비슷하다.
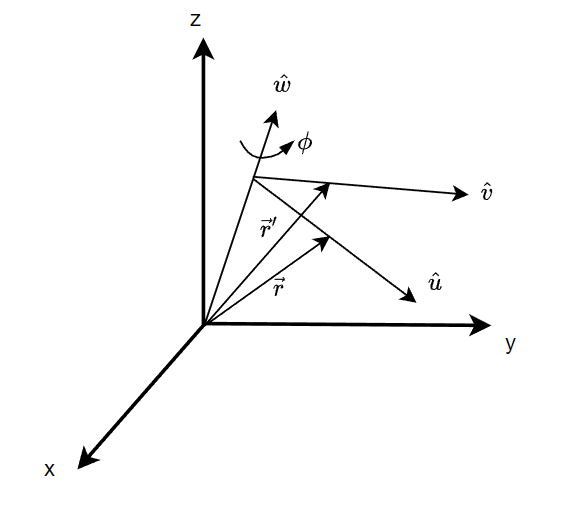
r-frame을 기준으로 b-frame의 회전축이 $\vec{w}$ 이고 회전각은 $\vec{\phi}$라고 하자. 이때 원래의 벡터 $\vec{r}$ 은 $\vec{r}'$로 회전된다.
이때 회전된 frame으로의 DCM은 아래와 같다.
$${}^{b}T_r = \begin{bmatrix} (1-cos\phi)l_1^2+cos\phi & (1-cos\phi)l_1l_2+l_3sin\phi & (1-cos\phi)l_1l_3-l_2sin\phi \\ (1-cos\phi)l_1l_2-l_3sin\phi & (1-cos\phi)l_2^2+cos\phi & (1-cos\phi)l_2l_3+l_1sin\phi \\ (1-cos\phi)l_1l_3+l_2sin\phi & (1-cos\phi)l_2l_3-l_1sin\phi & (1-cos\phi)l_3^2+cos\phi \end{bmatrix}$$
- Eigen Axis of DCM
Eigen Axis rotation이란, 회전축 벡터의 표현이 두 frame에 대해 같은 회전을 의미한다.
DCM ${}^{b}T_r$의 경우 회전축 $l$이
$$\vec{l} = {}^{b}T_r\vec{l}$$
를 만족할 때 eigen axis rotation이라고 한다. 이 때 $\vec{l}$은 eigen value가 1일 때의 eigen vector가 된다.
$$\vec{l}=\vec{l}_b=\vec{l}_r$$
eigen axis rotation의 경우 회전축을 표현하기가 용이하고, 센서로부터 값을 찾기 용이하다는 장점이 있다.
DCM Kinematics
r-frame에서 b-frame으로의 DCM ${}^{b}T_{r}$의 변화를 유도해 보자.
$$\frac{d}{dt} {}^{b}T_{r} $$
를 구하는 것이 목적이다. 이는 아래의 관계를 통해 쉽게 유도해 볼 수 있다.
$$\vec{r}_b={}^{b}T_{r}\vec{r}_r$$
$$\frac{d}{dt}|_b\vec{r}_b = {}^{b}T_{r} \frac{d}{dt}|_b\vec{r}_r+\frac{d}{dt}({}^{b}T_{r})\vec{r}_r $$
$$= {}^{b}T_{r}(\frac{d}{dt}|_r\vec{r}_r+\vec{w}_r \times \vec{r}_r)+\frac{d}{dt}({}^{b}T_{r})\vec{r}_r $$
이때 위성은 강체이므로 $\frac{d}{dt}|_b\vec{r}_b=0$ 이고, DCM에서는 회전만 고려하므로 Translation에 대한 항인 $\frac{d}{dt}|_r\vec{r}_r=0$이다.
그러므로
$$ \frac{d}{dt}({}^{b}T_{r})\vec{r}_r = -{}^{b}T_{r}(\vec{w}_r \times \vec{r}_r) = -\vec{w}_b\times({}^{b}T_r\vec{r}_r)=-[\vec{w}_b]_\times{}^{b}T_r\vec{r}_r$$
$$\downarrow$$
$$\frac{d}{dt}{}^{b}T_{r}=-[\vec{w}_b|_b]_\times{}^{b}T_r$$
$$[\vec{w}]_\times=\begin{bmatrix} 0 & -w_3 & w_2 \\ w_3 & 0 & -w_1 \\ -w_2 & w_1 & 0 \end{bmatrix} $$
** 이때 $\vec{w}_b$는 b-frame에서 표현된 b-frame의 각속도 이다. $\vec{w}_b|_b={}^{b}T_r\vec{w}_b|_r$
Quaternion Kinematics
위성의 현재 쿼터니안을 $\bar{q}=\begin{bmatrix} \vec{q} & q_4 \end{bmatrix}$라 하고 각속도를 $\vec{w}$라고 하자.
쿼터니안 변화율은 다음과 같다.
$$\dot{\bar{q}}=\frac{1}{2} \begin{bmatrix} 0 & w_z & -w_y & w_x \\ -w_z & 0 & w_x & w_y \\ w_y & -w_x & 0 & w_z \\ -w_x & -w_y & -w_z & 0 \end{bmatrix}\bar{q}$$
이는 아래와 같이 quaternion product로 나타낼 수 있다.
$$\dot{\bar{q}}=\frac{1}{2}\begin{bmatrix} \vec{w} \\ 0 \end{bmatrix} \otimes \bar{q}$$
Exercise
위성의 자세와 각속도가 다음과 같이 주어졌다.
Initial attitude : $\bar{q}=[0,0,0,1]$
Constant body anguler rate : $\vec{w} = [1,-2,1]^T$
Problem 1. Find euler angle rate
Problem 2. Find DCM rate
Problem 3. Find quaternion rate
3가지를 찾을 후 비교해 보기를 바란다. 세 결과 모두 하나의 자세를 나타내고 있어야 한다.
또한 3 경우에 대해 컴퓨팅 속도를 비교해 보기를 바란다.
이 3 가지의 Kinematics는 제어기에 사용될 D-control의 input으로 사용될 수 있다. 추후 글에서 다루겠지만 3가지 모두 control law를 만들어 낼 수 있다. 그러나 분명히 각각의 장단점이 존재한다. 그 장단점이 무엇이고 왜 quaternion control이 매우 효과적인지 앞으로 다루게 될 것이다.
