Intro
앞 글에서 위성의 Attitude Kinematics를 공부했다. Kinematics와 Dynamics의 가장 큰 차이점은 힘(Force)의 유무 이다. Kinematics에서는 물체에 작용하는 힘을 고려하지 않은 채 위성 자세의 변화를 고려했다. 여기서 힘을 고려하지 않았다는 것은 힘이 작용하지 않았다라는 것이 아니라, 힘과 운동에 대한 물리적인 관계를 고려하지 않았다는 것이다. 힘은 이미 작용해서 물체의 운동을 발생시켰고, 그 이후 물체의 운동을 다루는 것이 Kinematics이다. 그렇기 때문에 Kinematics는 운동의 기하학적 관계를 많이 다루게 된다.
반면 Dynamics는 Kinematics와 Kinetic이 모두 포함된 뜻으로, Kinetic에서는 물체에 힘이 작용한 순간부터 운동이 발생하기 까지의 과정을 다룬다. 즉 Dynamics는 물체에 작용하는 힘과 그로인해 발생하는 운동, 운동의 변화를 모두 다루는 학문이다. Dynamics를 통해 힘이 물체의 운동을 어떻게 변화시키는지 파악하고, 이를 응용하여 물체를 원하는대로 회전, 이동 시키기 위해 어떠한 힘을 가해주어야 하는지 공부하게 될 것이다.
Basic Vector Mechanics
벡터의 기본 연산이다. 벡터는 기본적으로 크기와 방향을 갖는 물리량이다. 그러므로 벡터에서 크기와 방향은 매우 중요한 정보라고 할 수 있다. 그러나 동역학에서는 이것만큼 중요한 것이 있다. 바로 벡터가 어디에서 정의되었는가 이다. 벡터의 중심은 어디이고 벡터가 표현된 좌표계는 어디인지는 동역학에서 빼놓을 수 없는 중요한 정보이다. 벡터의 중심, 벡터의 좌표계가 벡터 동역학을 표현하는데에 있어서 굉장히 중요한 요소이기 때문이다.
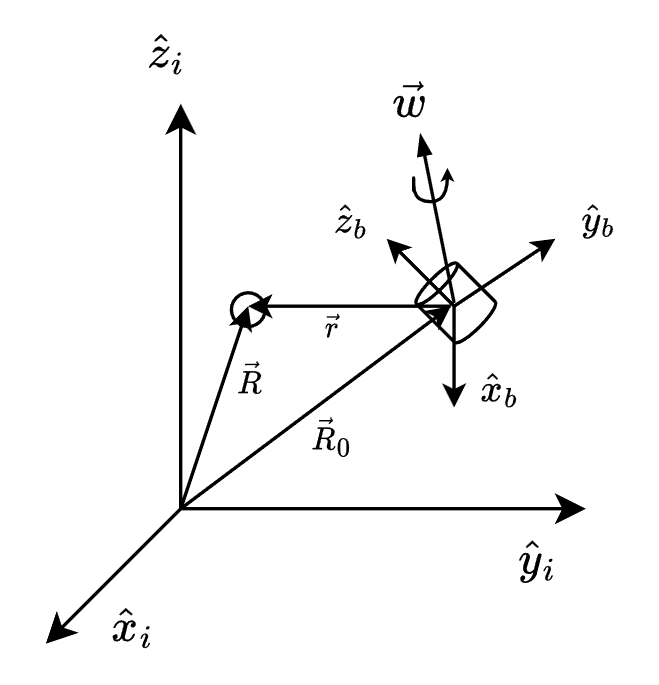
그림과 같이 밑첨자 i가 쓰인 관성좌표계와 밑첨자 b가 쓰인 body 좌표계가 있다. 이 때 벡터 미분은 아래와 같다.
$$\vec{R}=\vec{R}_0+\vec{r}$$
$$\dot{{\vec{R}}} = \dot{\vec{R}}_0+\dot{\vec{r}}_b+\vec{w} \times \vec{r}$$
$$\ddot{\vec{R}} = \ddot{\vec{R}}_0 + \ddot{\vec{r}}_b+2(\vec{w}\times\dot{\vec{r}}_b)+\vec{w} \times (\vec{w} \times \vec{r})$$
이때, 항등식의 단위는 모든 항이 같아야 하듯이, 벡터가 표현된 좌표계는 모두 동일해야 한다. 즉, 위 식은 단일 frame에서만 유효하다. 예를들어 $\vec{R}$은 i-frame에서 표현되어 있고 $\vec{r}$은 b-frame에서 표현되어 있다면 위식은 성립하지 않는다. 각 항의 모든 벡터가 i-frame에서 표현되어 있거나 모든 벡터가 b-frame에서 표현되어 있어야 한다.
Angular Momentum and Torque
Dynamics는 힘과 운동의 관계 라고 하였다. 여기서는 토크과 각 운동량 그리고 회전의 관계에 대해 공부해 보자.
- Angular Momentum 정의
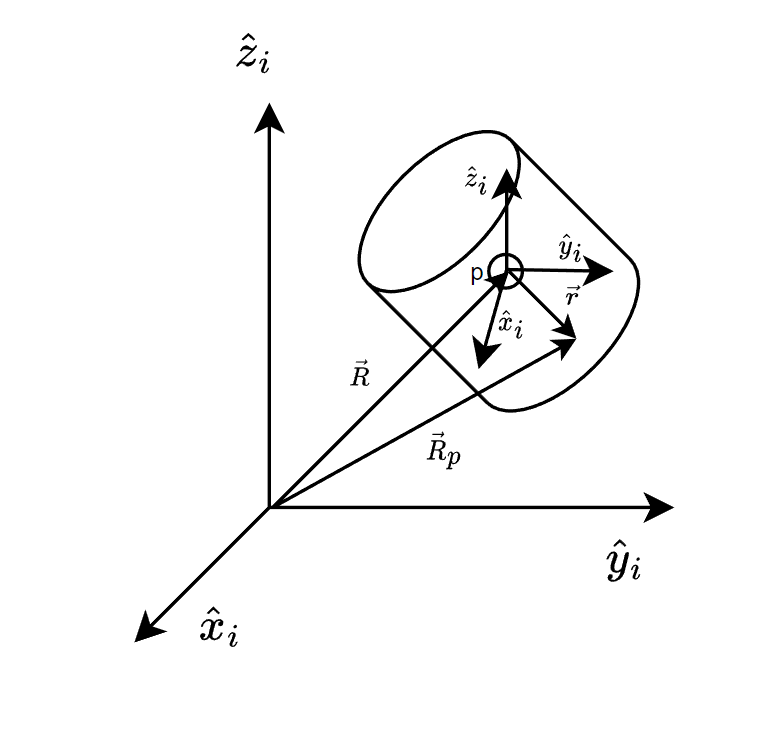
강체 B의 질량 중심 P로부터 강체의 질량소($dm$)까지의 거리를 $\vec{r}$이라 하자. 이때 각 운동량은 다음과 같이 정의한다.
$$\vec{H}=\int_B \vec{r} \times \frac{d}{dt}\vec{r} dm = \int_B\vec{r} \times \dot{\vec{r}}dm$$
- 각 운동량 시간 변화율
$$\dot{\vec{H}}=\int_B \dot{\vec{r}} \times \dot{\vec{r}}dm + \int_B\vec{r} \times \ddot{\vec{r}}dm = \int_B\vec{r} \times \ddot{\vec{r}}dm $$
$$=\int_B \vec{r} \times (\ddot{\vec{R}}-\ddot{\vec{R}}_p) dm$$
$$=\int_B \vec{r} \times \ddot{\vec{R}}dm + \ddot{R}_p \times \int_B\vec{r}dm$$
무게중심의 정의에서 $ \int_B\vec{r}dm=0$ 이므로
$$\dot{\vec{H}} = \int_B \vec{r} \times \ddot{\vec{R}}dm = \vec{T}$$
그러므로 각운동량의 변화율은 토크와 동일하다. 이 또한 벡터 항등식 이므로 각운동량의 변화율과 토크 벡터가 표현된 좌표계는 동일해야 수식이 성립한다.
Moment of Inertia
힘과 가속도 사이에 질량 이라는 상수가 있듯이, 토크과 각가속도 사이에도 관성 모멘트라는 상수가 존재한다. 이해하는데에 있어서 관성 모멘트는 질량과 같은 물리적 성질을 갖는다 라고 보아도 무방하다. 질량이 클 수 록 움직이는데 큰 힘이 필요하고, 마찬가지로 관성 모멘트가 클 수록 회전시키는데 큰 토크가 필요하다. 관성모멘트는 강체가 갖는 고유의 물리량 이다. 그러니 관성모멘트는 기본적으로 body frame을 기준으로 표현된다. 이 값을 이용하기 위해 각 운동량을 body frame을 기준으로 표현하면 다음과 같다.
$$\vec{H}_b=\int_B\vec{r}_b \times \dot{\vec{r}}_b dm = \int_B\vec{r}_b \times (\vec{w}_b \times \vec{r}_b)dm$$
벡터 외적은 전개한 후 관성 모멘트를 이용하여 나타내면 다음과 같다.
$$\vec{H}_b=\begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{bmatrix}\begin{bmatrix} w_x \\ w_y \\ w_z \end{bmatrix} = I\vec{w}_b$$
Euler's equation
Body frame에서 표현된 각 운동량의 미분에 vector mechanics를 적용하면 다음과 같다.
$$\frac{d\vec{H}_b}{dt}|_i=\frac{d\vec{H}_b}{dt}|_b + \vec{w} \times \vec{H}$$
위에서 정의한 각 운동량의 변화량과 토크, 관성 모멘트의 관계를 이용하면 각 운동량의 운동 방정식을 얻을 수 있다.
$$T_b=I\dot{\vec{w}}_b + \vec{w}_b \times I\vec{w}_b$$
관성 모멘트 $I$는 일반적으로 body frame을 기준으로 정의되기 때문에, 이 식은 body frame에서 계산되어야 한다..
관성 좌표계를 기준으로 계산하기 위해서는 관성 모멘트를 해당 좌표계에서 표현해야 한다.
Intro
앞 글에서 위성의 Attitude Kinematics를 공부했다. Kinematics와 Dynamics의 가장 큰 차이점은 힘(Force)의 유무 이다. Kinematics에서는 물체에 작용하는 힘을 고려하지 않은 채 위성 자세의 변화를 고려했다. 여기서 힘을 고려하지 않았다는 것은 힘이 작용하지 않았다라는 것이 아니라, 힘과 운동에 대한 물리적인 관계를 고려하지 않았다는 것이다. 힘은 이미 작용해서 물체의 운동을 발생시켰고, 그 이후 물체의 운동을 다루는 것이 Kinematics이다. 그렇기 때문에 Kinematics는 운동의 기하학적 관계를 많이 다루게 된다.
반면 Dynamics는 Kinematics와 Kinetic이 모두 포함된 뜻으로, Kinetic에서는 물체에 힘이 작용한 순간부터 운동이 발생하기 까지의 과정을 다룬다. 즉 Dynamics는 물체에 작용하는 힘과 그로인해 발생하는 운동, 운동의 변화를 모두 다루는 학문이다. Dynamics를 통해 힘이 물체의 운동을 어떻게 변화시키는지 파악하고, 이를 응용하여 물체를 원하는대로 회전, 이동 시키기 위해 어떠한 힘을 가해주어야 하는지 공부하게 될 것이다.
Basic Vector Mechanics
벡터의 기본 연산이다. 벡터는 기본적으로 크기와 방향을 갖는 물리량이다. 그러므로 벡터에서 크기와 방향은 매우 중요한 정보라고 할 수 있다. 그러나 동역학에서는 이것만큼 중요한 것이 있다. 바로 벡터가 어디에서 정의되었는가 이다. 벡터의 중심은 어디이고 벡터가 표현된 좌표계는 어디인지는 동역학에서 빼놓을 수 없는 중요한 정보이다. 벡터의 중심, 벡터의 좌표계가 벡터 동역학을 표현하는데에 있어서 굉장히 중요한 요소이기 때문이다.

그림과 같이 밑첨자 i가 쓰인 관성좌표계와 밑첨자 b가 쓰인 body 좌표계가 있다. 이 때 벡터 미분은 아래와 같다.
$$\vec{R}=\vec{R}_0+\vec{r}$$
$$\dot{{\vec{R}}} = \dot{\vec{R}}_0+\dot{\vec{r}}_b+\vec{w} \times \vec{r}$$
$$\ddot{\vec{R}} = \ddot{\vec{R}}_0 + \ddot{\vec{r}}_b+2(\vec{w}\times\dot{\vec{r}}_b)+\vec{w} \times (\vec{w} \times \vec{r})$$
이때, 항등식의 단위는 모든 항이 같아야 하듯이, 벡터가 표현된 좌표계는 모두 동일해야 한다. 즉, 위 식은 단일 frame에서만 유효하다. 예를들어 $\vec{R}$은 i-frame에서 표현되어 있고 $\vec{r}$은 b-frame에서 표현되어 있다면 위식은 성립하지 않는다. 각 항의 모든 벡터가 i-frame에서 표현되어 있거나 모든 벡터가 b-frame에서 표현되어 있어야 한다.
Angular Momentum and Torque
Dynamics는 힘과 운동의 관계 라고 하였다. 여기서는 토크과 각 운동량 그리고 회전의 관계에 대해 공부해 보자.
- Angular Momentum 정의

강체 B의 질량 중심 P로부터 강체의 질량소($dm$)까지의 거리를 $\vec{r}$이라 하자. 이때 각 운동량은 다음과 같이 정의한다.
$$\vec{H}=\int_B \vec{r} \times \frac{d}{dt}\vec{r} dm = \int_B\vec{r} \times \dot{\vec{r}}dm$$
- 각 운동량 시간 변화율
$$\dot{\vec{H}}=\int_B \dot{\vec{r}} \times \dot{\vec{r}}dm + \int_B\vec{r} \times \ddot{\vec{r}}dm = \int_B\vec{r} \times \ddot{\vec{r}}dm $$
$$=\int_B \vec{r} \times (\ddot{\vec{R}}-\ddot{\vec{R}}_p) dm$$
$$=\int_B \vec{r} \times \ddot{\vec{R}}dm + \ddot{R}_p \times \int_B\vec{r}dm$$
무게중심의 정의에서 $ \int_B\vec{r}dm=0$ 이므로
$$\dot{\vec{H}} = \int_B \vec{r} \times \ddot{\vec{R}}dm = \vec{T}$$
그러므로 각운동량의 변화율은 토크와 동일하다. 이 또한 벡터 항등식 이므로 각운동량의 변화율과 토크 벡터가 표현된 좌표계는 동일해야 수식이 성립한다.
Moment of Inertia
힘과 가속도 사이에 질량 이라는 상수가 있듯이, 토크과 각가속도 사이에도 관성 모멘트라는 상수가 존재한다. 이해하는데에 있어서 관성 모멘트는 질량과 같은 물리적 성질을 갖는다 라고 보아도 무방하다. 질량이 클 수 록 움직이는데 큰 힘이 필요하고, 마찬가지로 관성 모멘트가 클 수록 회전시키는데 큰 토크가 필요하다. 관성모멘트는 강체가 갖는 고유의 물리량 이다. 그러니 관성모멘트는 기본적으로 body frame을 기준으로 표현된다. 이 값을 이용하기 위해 각 운동량을 body frame을 기준으로 표현하면 다음과 같다.
$$\vec{H}_b=\int_B\vec{r}_b \times \dot{\vec{r}}_b dm = \int_B\vec{r}_b \times (\vec{w}_b \times \vec{r}_b)dm$$
벡터 외적은 전개한 후 관성 모멘트를 이용하여 나타내면 다음과 같다.
$$\vec{H}_b=\begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{bmatrix}\begin{bmatrix} w_x \\ w_y \\ w_z \end{bmatrix} = I\vec{w}_b$$
Euler's equation
Body frame에서 표현된 각 운동량의 미분에 vector mechanics를 적용하면 다음과 같다.
$$\frac{d\vec{H}_b}{dt}|_i=\frac{d\vec{H}_b}{dt}|_b + \vec{w} \times \vec{H}$$
위에서 정의한 각 운동량의 변화량과 토크, 관성 모멘트의 관계를 이용하면 각 운동량의 운동 방정식을 얻을 수 있다.
$$T_b=I\dot{\vec{w}}_b + \vec{w}_b \times I\vec{w}_b$$
관성 모멘트 $I$는 일반적으로 body frame을 기준으로 정의되기 때문에, 이 식은 body frame에서 계산되어야 한다..
관성 좌표계를 기준으로 계산하기 위해서는 관성 모멘트를 해당 좌표계에서 표현해야 한다.
