이번 시간에는 궤도 미분 방정식을 정리하고 그 중 궤도를 나타내는 6개의 요소를 학습할 것이다.
이어서 6개의 요소와 6개의 상태 벡터( 위치, 속도 ) 의 관계가 무엇인지 학습한다.
Recap Orbit Equation
- Dynamics
$$\ddot{\vec{r}} = -\frac{\mu}{r^3}\vec{r}$$
$$r_o = x_0i + y_0j + z_0k $$
$$v_0 = \dot{x}_0i + \dot{y}_0j + \dot{z}_0k$$
- Solution ( Orbit Equation)
$$r = \frac{H^2/\mu}{1+ecos(\nu)}$$
$$\vec{H} = \vec{r} \times \vec{v} = const$$
$$\vec{e} = [\dot{\vec{r}} \times \vec{H} - \mu\frac{\vec{r}}{r}]/ \mu = const$$
$$\begin{cases} tan\frac{1}{2}\nu = \sqrt{\frac{1+e}{1-e}}tan\frac{1}{2}E \\ n(t-T_0) = E-sinE \end{cases}$$
$$\epsilon = \frac{1}{2}v^2-\frac{\mu}{r} = -\frac{\mu}{2a} = const $$
이 식을 통해 초기 초건 $r_0, v_0$가 주어졌을 때 궤도 방정식의 해를 구할 수 있다.
그런데, Solution에 있는 궤도 방정식은 스칼라 식이다. 벡터 미분 방정식의 해는 6개의 요소로 이루어져야 한다! 허나 위에서 알 수 있는 것은 위치와 속도의 크기 두 개만 알 수 있다. 그렇다면 이 스칼라 값을 어떻게 6개의 상태 벡터로 바꿀 수 있을까? 생각해보자.
Orbit Plane
그것은 바로 $\vec{H}$와 $\vec{e}$로부터 알 수 있다. $\vec{H}$와 $\vec{e}$의 의미가 무엇이었는지 기억이 나는가.
$\vec{H}$는 위치와 속도의 외적, 즉 궤도 평면의 Normal Vector를 의미한다. $\vec{e}$는 궤도의 근지점 벡터를 의미했었다. 기억이 나지 않는다면 이전의 글을 다시 보고 오기를 바란다.

우리가 현재 알고 있는 궤도는 위 그림과 같다. 즉 궤도 평면 위에서 위성의 위치와 속도를 알고 있는 것이다. 이 평면을 PQW 평면이라고 부른다.
이를 3차원 공간(관성 좌표계)에서 그리면 아래와 같다.

즉, 우리가 구했던 위치와 속도는, 3차원 공간상에 존재하는 위성의 위치와 속도를 나타내는 것이 아니라 궤도 평면 안에서의 위성의 위치와 속도를 나타내고 있는 것이다.
$\vec{H}$는 궤도면에 수직으로 존재하고, $\vec{e}$는 단반경 방향을 향하는 벡터임을 함께 나타내 주었다.
여기서 새로운 변수들이 추가되었다. 바로 $i, \omega, \vec{n}, \Omega$이다.
PQW에서의 위치와 속도를 어떻게 관성 좌표계에서 표현할 수 있을까. 좌표계 변환 행렬을 이요하면 된다. 새롭게 추가된 변수들이 좌표계 변환을 위한 각도이다. 이 각도들은 모두 $\vec{H}$와 $\vec{e}$ 로부터 찾을 수 있다.
좌표계 변환에 대해 익숙하지 않다면
2023.03.07 - [비행동역학 및 제어] - [비행동역학 및 제어] 1. 기준 좌표계 및 좌표계 변환
2023.04.08 - [비행동역학 및 제어] - [비행동역학 및 제어] 2. 회전 변환 행렬 및 쿼터니안
이 두가지 글을 읽고 오길 바란다.
Orbit Elements
궤도면으로부터 3차원 궤도로의 좌표계 변환을 어떻게 수행할 수 있을까. 일반적으로 좌표계 변환에 있어서 3번의 오일러 회전이 필요하다. 그러므로 회전과 관련된 3개의 각도를 찾아야 한다. 이 세 각도가 $i, \omega, \Omega$ 이다.
- Inclination
$i$는 $\vec{H}$와 관성좌표계의 $z$축과의 각도로, 궤도의 경사각을 의미한다. 즉, 궤도가 얼마나 기울어져 있는지 나타내는 변수이다. 이때 회전축을 생각해보자. 회전축은 $\hat{k}$와 $\vec{H}$의 외적이 된다. 즉 회전축은 $\vec{n}$가 된다.
$$i = cos^{-1}(\frac{\vec{h} \cdot [0,0,1]}{|\vec{h}|})$$
inclination의 경사각의 범위는 $[0,\pi]$이다. z축에서 바라봤을 때 0~$0.5\pi$일때는 반시계방향, $0.5\pi ~ \pi$일때는 시계방향으로 회전한다.
- Right ascension of ascending node (raan)
raan($\vec{n}$)은 승교점 벡터로, 위성이 x-y평면 아래에서 위쪽으로 통과할때 지나는 x-y평면 위의 지점을 의미한다.
이 점은 기하학적으로 $\hat{k}$와 $\vec{H}$에 대해 수직한 지점이다. 그러므로 $\hat{k}$와 $\vec{H}$의 외적과 같다. 결과적으로 승교점 벡터는 궤도 경사각 회전에 대한 회전축이 된다.
승교점 각도 $\Omega$는 $\hat{i}$로부터 $\vec{n}$까지의 각도이다. x-y 평면에서의 회전이므로 회전축은 $\hat{k}$이다.
$$\vec{n} = \frac{[0,0,1] \times \vec{h}}{|\vec{h}|}$$
$$\Omega = tan^{-1}(\frac{n(2)}{n(1)})$$
$$0 \leq \Omega \leq 2\pi$$
이때 $tan^{-1}$는 quadrant ambiguity가 존재하기 때문에 $\vec{n}$에 따라 핸들링을 해주어야 한다.
- Argument of Perigee
위의 두 가지만으로 궤도를 정의하기엔 부족하다. 같은 경사각과 같은 승교점을 갖더라도 $\vec{e}$에 따라 여러가지의 궤도면이 나올 수 있기 때문이다. Argument of Perigee($\omega$)는 승교점 벡터에 대해 $\vec{e}$가 회전한 각도를 나타낸다. 즉, 궤도의 근지점 벡터가 어디인지 나타내는 파라미터 이다.
$$\omega = cos^{-1}(\frac{\vec{n} \cdot \vec{e} }{|\vec{n}| |\vec{e}|})$$
$$ 0 \leq \omega \leq 2\pi$$
$cos^{-1}$도 마찬가지로 quadrant ambiguity가 존재하기 때문에 핸들링을 해주어야 한다.
이렇게 세 가지 요소가 3차원 상에서 궤도 평면을 나타내는 각도가 된다. 여기에 추가로 3개의 요소 $a,e,\nu$를 더하면
궤도를 나타내는 6개의 요소가 된다. 이 6개의 요소를 궤도 6요소 또는 케플러 6요소 라고 한다.
$$\textit{Kepler's Orbit Elements : }a,e,\nu,i,\Omega,\omega$$
이 6가지를 알고 있으면 궤도 평면과 위성의 위치를 표현할 수 있다.
Orbit Frame Transformation
관성 좌표계에서 궤도 평면으로의 좌표계 변환을 생각해 보자. 관성좌표계의 3축은 $x,y,z$이고 궤도면의 3축은 $p,q,w$이다. 관성 좌표계를 궤도 평면으로 변환하기 위해서 $\Omega$ 회전, $inclination$회전, $\omega$회전을 순서대로 시행한다.


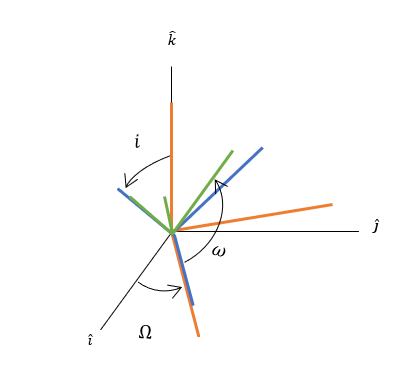
- Transform matrix
회전 변환 순서가 3($\Omega$)-1($i$)-3($\omega$)이므로 회전 변환 행렬은 아래와 같다.
$$C_I^{pqw} = R_3(\omega)R_1(i)R_1(\Omega)$$
$$=\begin{bmatrix} cos\omega & sin\omega & 0 \\ -sin\omega & cos\omega & 0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} 1&0&0 \\ 0&cosi & sini \\ 0& -sini & cosi \end{bmatrix} \begin{bmatrix} cos\Omega & sin\Omega & 0 \\ -sin\Omega & cos\Omega & 0 \\ 0&0&1 \end{bmatrix}$$
$$=$$\begin{bmatrix} cos(w)cos(\Omega)-sin(w)cos(i)sin(\Omega)& cos(w)sin(\Omega)+sin(w)cos(i)cos(\Omega)& sin(w)sin(i) \\ -sin(w)cos(\Omega)-cos(w)cos(i)sin(\Omega)& -sin(w)sin(\Omega)+cos(w)cos(i)cos(\Omega)&cos(w)sin(i) \\ sin(i)sin(\Omega)& -sin(i)cos(\Omega)& cos(i)\end{bmatrix}$$$$
이는 관성좌표계에서 pqw로의 회전 변환 행렬이 된다. 반대로 pqw에서 관성 좌표계로의 회전 변환 행렬은 위 행렬의 Transpose와 동일하다.
$$C_{pqw}^I = [C_I^{pqw}]^T$$
이제 pqw 평면에 존재하는 위성의 위치와 속도 벡터를 관성 좌표계에서 표현할 수 있다.
$$ r = \frac{H^2/ \mu}{1+ecos(\mu)}$$
$$r^{pqw} = rcos(\nu)\hat{p} + rsin(\nu)\hat{q} + 0\hat{w}$$
라고 한다면 관성좌표계에서 위성의 위치벡터는 아래와 같다.
$$r^I = C_{pqw}^I r^{pqw} = [C_I^{pqw}]^T r^{pqw}$$
속도 벡터는 궤도면에 접하는 방향 이므로 같은 방법으로 구할 수 있다.
결과적으로 궤도 6요소를 알고 있으면 관성좌표계에서 위성의 위치와 속도를 알아낼 수 있다.
반대로 관성좌표계에서 위성의 위치와 속도를 알고 있다면 궤도 6요소를 알아낼 수 있다.
To Do
이번 글에서는 궤도 6요소와 위성의 위치, 속도의 관계를 다루었다. 궤도 6요소는 궤도와 위성의 위치를 3차원 공간상에서 정의하기 위한 독립적인 요소들이고 직관적으로 궤도 형태를 이해할 수 있도록 한다. 이는 당연하게도 위성의 위치, 속도와 관련이 되어 있는데 이 둘의 관계를 다루었다. 궤도 6요소는 위성의 궤도를 정의하는 경우에 주로 사용되며 위치, 속도는 궤도상에서 위성의 움직임을 모델링하는데 주로 사용된다. 이 둘의 변환 관계는 궤도를 이해하는데에 있어서 중요한 개념이므로 잘 알고 있어야 한다.
이번 시간을 끝으로, 이체 문제에서 위성의 궤도에 대한 모델링을 끝마쳤다. 다음시간 부터는 이를 이용하여 지구 위성의 궤도 기동에 대해 다룰 것이다.
